2.1. Signaux à temps discret

2.1.1. Classes de Signaux

Definition 2.1 (Classes des signaux numériques)

Comme pour les signaux à temps continu, les signaux à temps discrets (ou signaux discret, ou signaux numériques) peuvent être déterministes (à énergie finie ou à puissance moyenne finie, périodiques ou non périodiques) ou aléatoires.

2.1.1.1. Signaux Déterministes à temps discret

On parlera de signal déterministe à temps discret pour désigner une suite numérique de \(\mathbb{Z}\) dans \(\mathbb{C}\) : \(x(n) \in \mathbb{C}\) avec \(n \in \mathbb{Z}\). Il s’agit ici d’un signal à une variable ou monodimensionnel mais un signal numérique peut également être multidimenssionnel. Nous avons, par exemple, dans le chapitre précédent des images définies par des suites numérique \(x(n,m) \in \mathbb{N}\), représentant les niveaux de gris des pixels de l’image pour chaque position \((m,n)\), avec \(n, m \in \mathbb{N}\).

Parmi les signaux déterministes à temps discret nous retrouvons les catégories suivantes :

Definition 2.2 (Classes de signaux déterministes à temps discret)

• Signaux déterministes à temps discret à énergie finie :

  \[E=\sum_{n=-\infty}^{+\infty} \left|x(n)\right|^2 < +\infty\]

• Signaux déterministes à temps discret à puissance moyenne finie non périodiques :

  \[P=\lim_{n \rightarrow \infty} \frac{1}{2N+1} \sum_{n=-N}^{N} \left|x(n)\right|^2 < +\infty\]

• Signaux déterministes à temps discret à puissance moyenne finie périodiques :

  \[P=\frac{1}{N} \sum_{n=O}^{N} \left|x(n)\right|^2 < +\infty\]

  en considérant un signal discret périodique, de période \(N\) : \(x(n+N)=x(n)\).

2.1.1.2. Signaux Aléatoires à temps discret

Un processus aléatoire discret \(X\) est décrit par ses propriétés statistiques, en particulier par :

• sa moyenne (moment d’ordre \(1\)) :

  \[m_X(n)=E\left[X(n)\right]\]

• sa fonction d’autocorrélation (moment d’ordre \(2\)) :

  \[R_X(k,n)=E\left[X(n)x^*(n-k)\right]\]

2.1.2. Quelques propriétés

Property 2.1

1. Périodicité :

   Un signal discret est périodique, de période \(N\) si \(x(n+N)=x(n), \; \forall n \in \mathbb{Z}\).

2. Symétrie, symétrie hermitienne :

   • Un signal discret réel est symétrique, ou pair, si \(x(-n)=x(n), \; \forall n \in \mathbb{Z}\), antisymétrique, ou impair, si \(x(-n)=-x(n) \; \forall n \in \mathbb{Z}\).

   • Un signal discret complexe possède la propriété de symétrie hermitienne si \(x(-n)=x^*(n), \; \forall n \in \mathbb{Z}\).

3. Translation (ou retard) :

   Un signal discret \(x(n)\) translaté (retardé) de \(k\) éhantillons s’écrit \(x(n-k)\).

4. Stationnarité :

   Un processus aléatoire discret, \(X\), est stationnaire si ses moments sont invariants pour tout changement de l’origine des temps. Il l’est au second ordre si sa moyenne et sa fonction d’autocorrélation sont indépendantes de \(n\) : \(m_X(n)=m_X\) et \(R_X(k,n)=R_X(k)\).

5. Ergodicité :

   Un processus aléatoire discret, \(X\), est ergodique si ses moments statistiques sont identiques à ses moments temporels. Cette dernière propriété est importante car elle permet d’étudier le processus en utilisant une de ses réalisations, chaque réalisation du processus aléatoire à temps discret étant un signal à temps discret déterministe.

2.1.3. Quelques signaux particuliers

Definition 2.3 (Dirac numérique)

Le Dirac numérique, ou impulsion unité, est défini par :

\[\begin{split} \delta(k) = \left\{ \begin{array}{rl} 1 & \mbox{si } k=0\\ 0 & \mbox{sinon} \\ \end{array} \right. \; \end{split}\]

Definition 2.4 (Echelon unité)

L’échelon unité, ou fonction de Heaviside, est défini en numérique par :

\[\begin{split} u(k) = \left\{ \begin{array}{rl} 1 & \mbox{si } k \geq 0\\ 0 & \mbox{sinon} \\ \end{array} \right. \; \end{split}\]

Definition 2.5 (Fonction signe)

La fonction signe est définie en numérique par :

\[\begin{split} sign(k) = \left\{ \begin{array}{rl} -1 & \mbox{si } k < 0\\ 0 & \mbox{si } k = 0\\ +1 & \mbox{si } k > 0 \\ \end{array} \right. \; \end{split}\]

2.1.4. Représentation des signaux à temps discret

On utilise généralement une représentation du signal numérique sous la forme d’un tableau :

\[x=\left[x(0)...x(N-1)\right]\]

pour des signaux à une dimension, avec \(x(n)\) qui représente la valeur du signal pour l’indice \(n\) (soit en réalité l’échantillon \(x(nT_e)\) de signal).

Ou bien sous la forme d’une matrice :

\[\begin{split}x=\begin{pmatrix} x(0,0) & ... & x(0,M-1) \\ x(1,0) & ... & x(1,M-1) \\ & ... & \\ x(N-1,0) & ... & x(N-1,M-1) \end{pmatrix}\end{split}\]

pour des signaux bidimensionnels, par exemple pour une image où \(x(i,j)\) représente la valeur du pixel sur la ligne \(i\) et colonne \(j\).

On peut aussi représenter le signal de manière graphique en traçant les valeurs du tableau en fonction de ses indices \(n\), ou bien en fonction du temps, en introduisant la variable \(T_e\), si celle-ci est connue, au niveau de l’échelle des absisses.

Si nous prenons l’exemple d’une fonction porte numérique :

\[\begin{split} x(k) = \left\{ \begin{array}{rl} 1 & \mbox{pour } k=0 \; \text{à} \; N-1\\ 0 & \mbox{ailleurs} \\ \end{array} \right. \; \end{split}\]

Nous pouvons la représenter, par exemple pour \(N=7\), à l’aide du tableau suivant \(\left[1 \; 1 \; 1 \; 1 \; 1 \; 1 \; 1 \right]\), ou bien la tracer avec une échelle en numéros d’indice ou en temps, comme le montre la figure suivante.

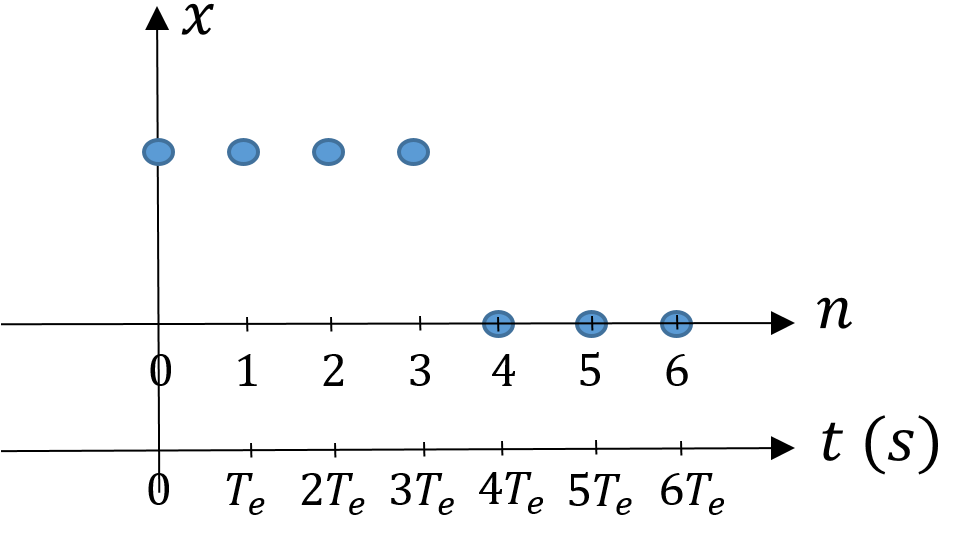
Fig. 2.1 Exemple de tracé d’une fonction porte numérique composée de \(7\) échantillons.