De la TF à la TFD
Contents
3.1. De la TF à la TFD#
3.1.1. Introduction#
Un signal en numérique est un tableau de points contenant un nombre fini, \(N\), de valeurs de signal : \(\left[x(0) \; x(1) \cdots ; x(N-1)\right]\), le \(k^{\text{ième}}\) élément \(x(k)\) représentant en réalité \(x(kT_e)\) si on considère un échantillonnage temporel périodique de période \(T_e\). On travaille donc avec des signaux échantillonnés et limités dans le temps et il n’est pas possible d’utiliser l’expression donnée précédemment pour \(X(f)\) pour déterminer leurs transformées de Fourier. Des approximations doivent être effectuées à partir de cette expression pour obtenir un outil numérique capable d’estimer une représentation fréquentielle et les effets induits par ces approximations doivent être connus de manière à être capable de mener correctement une analyse spectrale en numérique.
L’objectif de ce paragraphe va être de lister les approximations à réaliser pour passer de la Transformée de Fourier (TF), définie par l’expression précédente de \(X(f)\), à la Transformée de Fourier numérique ou Discrète (TFD) qui sera finalement donnée par l’expression suivante :
3.1.2. Echantillonnage#
Un signal numérique est forcément échantillonné :
L’échantillonnage du signal va avoir pour effet de périodiser sa transformée de Fourier, qui est approchée par la somme des aires des rectangles sous la courbe, au facteur \(T_e\) près :
\(X_1(f)\) est bien périodique de période \(F_e=\frac{1}{T_e}\) : \(X_1(f+F_e)=X_1(f)\). On devra donc faire attention au respect du théorème d’échantillonnage de Shannon pour ne pas provoquer de recouvrement lors de l’échantillonnage. On devra également faire attention à la manière dont on lit la TF du signal échantillonné. En effet si elle est observée sur une période, entre \(0\) et \(F_e\), la partie positive du spectre sera observée entre \(0\) et \(F_e/2\), tandis que la partie négative le sera entre \(F_e/2\) et \(F_e\).
Definition 3.1 (TF du signal échantillonné)
L’échantillonnage du signal a pour effet de périodiser sa transformée de Fourier. On devra donc faire attention au respect du théorème d’échantillonnage de Shannon mais également à l’analyse de la TF du signal échantillonné qui est classiquement observée sur une période côté fréquences positives (utilisation de fft sous matlab par exemple).
3.1.3. Limitation de la durée du signal à \(N\) points#
Un signal numérique est forcément observé sur un nombre fini de points :
Cette connaissance du signal sur un nombre limité de points (dimension du tableau représentant le signal numérique) conduit à une distorsion de la transformée de Fourier :
qui donne :
où \(W_1(f)=\sum_{k=-\infty}^{+\infty} w(kT_e)e^{-j 2 \pi f kT_e}\) avec \(w(kT_e)=\left\{ \begin{array}{ll} 1 & \hbox{k=0, ..., N-1} \\ 0 & \hbox{ailleurs.} \end{array} \right.\)
Cette distorsion de la transformée de Fourier implique un pouvoir séparateur limité pour l’analyse spectrale (possibilité de dissocier \(2\) motifs spectraux de fréquences proches) et un certain taux d’ondulation (des ondulations apparaissent autour des transitions brutales du spectre : phénomène de Gibbs).
Ces paramètres (pouvoir séparateur et taux d’ondulation) sont liés à la forme de \(W_1(\widetilde{f})\), plus précisément à la largeur de son lobe principal et à l’amplitude de ses lobes secondaires (voir Fig. 3.1).
On pourra faire varier le pouvoir séparateur et le taux d’ondulation de l’analyse spectrale en tronquant le signal étudié avec différentes fenêtres \(w(kT_e)\), autres que rectangulaire (fenêtres de pondération ou d’apodisation), de manière à obtenir différentes formes pour \(W_1(f)\) et donc différentes versions de la TFD du même signal.
La Fig. 3.2 présente quelques fenêtres classiques d’apodisation, tandis que la Fig. 3.3 présente leurs transformées de Fourier. On peut constater que les lobes centraux sont plus ou moins larges, conduisant à un pouvoir séparateur plus ou moins grand pour l’analyse spectrale. On peut également constater que les lobes secondaires sont plus ou moins atténués, conduisant à un taux d’ondulation plus ou moins grand pour l’analyse spectrale. Lorsque des fenêtres autres que rectangulaires sont utilisées on parle de transformée de Fourier pondérée.
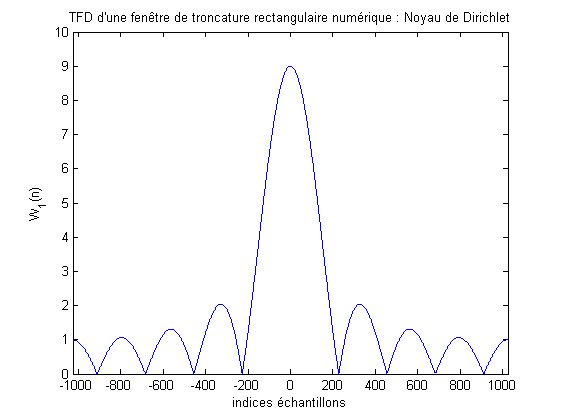
Fig. 3.1 Transformées de Fourier de la fenêtre rectangulaire : Noyau de Dirichlet.#
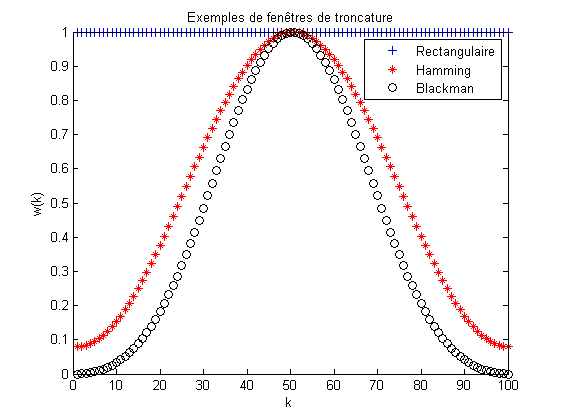
Fig. 3.2 Quelques exemples de fenêtres d’apodisation.#
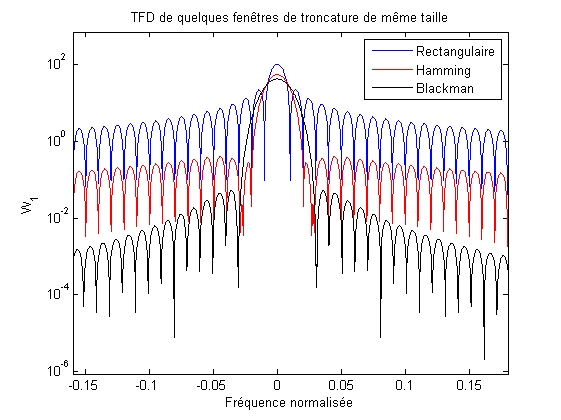
Fig. 3.3 Transformées de Fourier de quelques fenêtres de troncature.#
Property 3.1 (TF d’un signal à durée limitée)
La connaissance du signal sur un nombre limité de points conduit à une distorsion de la transformée de Fourier attendue : convolution par la TF de la fenêtre modélisant la troncature du signal. Cette distorsion implique un pouvoir séparateur limité pour l’analyse spectrale numérique et un certain taux d’ondulation. Elle dépend de la fenêtre utilisée et on réalisera donc chaque analyse spectrale en utilisant plusieurs fenêtres de troncature (fenêtres de pondération) pour obtenir différentes visualisations de la TF d’un même signal afin d’en extraire différentes informations.
La Fig. 3.4 présente un exemple dans lequel les différentes fenêtres utilisées permettent de mettre en exergue différentes composantes spectrales. Mais quel est donc le signal qui pourrait correspondre à ces différents spectres ?
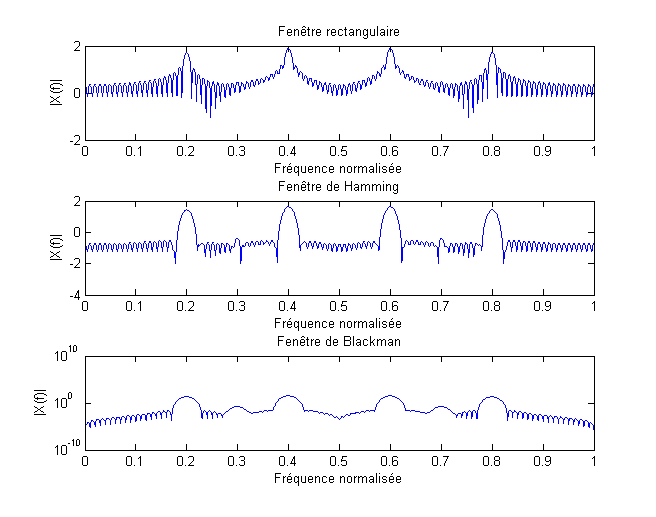
Fig. 3.4 Différentes versions de la transformée de Fourier d’un même signal.#
3.1.4. Calcul de \(N\) points du spectre#
Tout comme le signal numérique ne peut pas être à temps continu, il ne sera possible de calculer qu’un nombre fini d’échantillons de la TFD :
En considérant que l’on calcule, sur une période \(F_e\), un nombre de point de la TFD identique au nombre \(N\) de points de signal (réversibilité de l’algorithme), on obtient un pas de calcul \(\Delta f=\frac{F_e}{N}\) et donc une transformée de Fourier discrète qui s’écrit :
Le fait de ne pouvoir calculer qu’un certain nombre de points de la transformée de Fourier numérique a un impact sur la résolution de l’analyse spectrale. Celle-ci sera liée au nombre de points calculés sur une période de la TFD : pas de calcul \(\Delta f = \frac{F_e}{N}\). \textcolor{ocre}{\textbf{Afin d’augmenter la résolution spectrale, on pourra utiliser une technique d’interpolation fréquentielle, la plus connue et utilisée étant celle du Zero Padding.}} On construit un nouveau signal, à partir du signal \(x(kT_e)\) donné sur \(N\) points, en le prolongeant par des zéros :
La TFD de ce nouveau signal :
dispose d’un pas de calcul plus fin : \(\frac{F_e}{MN}\). On calcule \(MN\) points distants de \(\frac{F_e}{MN}\) entre \(0\) et \(F_e\) (une période de la TFD), au lieu de \(N\) points distants de \(\frac{F_e}{N}\) entre \(0\) et \(F_e\). La résolution spectrale est donc améliorée.
Les Fig. 3.5 et Fig. 3.6 proposent des tracés du module de la transformée de Fourier numérique d’un cosinus numérique observé sur \(N=1000\) points, pour différentes valeurs du paramètre \(MN\). Ces tracés sont donnés avec une échelle en fréquences normalisées : \(\widetilde{f}=\frac{f}{F_e}\).
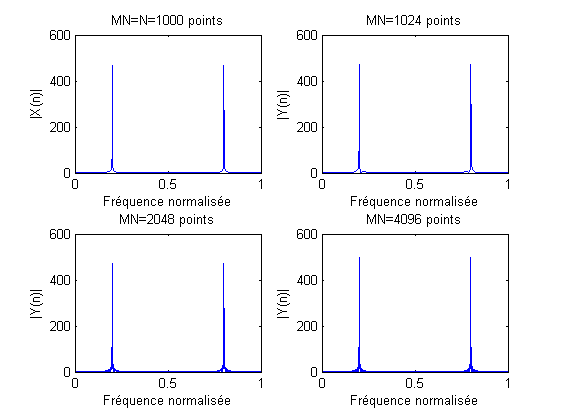
Fig. 3.5 Transformées de Fourier d’un cosinus de fréquence normalisée \(0.2\) pour différentes valeurs du paramètre de zero padding.#
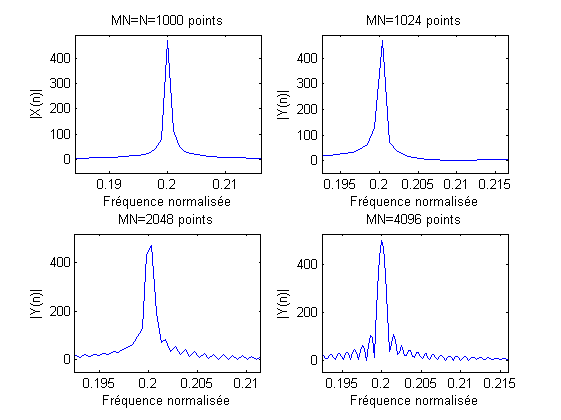
Fig. 3.6 Transformées de Fourier d’un cosinus de fréquence normalisée \(0.2\) pour différentes valeurs du paramètre de zero padding : zoom un pic de la Fig. 3.5#
Un autre impact de la discrétisation fréquentielle est une périodisation temporelle. On doit, en effet, considérer en numérique que les signaux sont périodisés, de même que leurs transformées de Fourier. Ce dernier point a une conséquence importante : cela ne permet pas de conserver à la TFD la propriété très intéressante de la TF qui consiste à transformer un produit de convolution en produit (et inversement). En effet, comme nous le verrons par la suite (sec_proprietes), la transformée de Fourier Discrète transforme un produit en produit de convolution circulaire, c’est-à-dire en produit de convolution entre des signaux périodisés. Néanmoins, il est possible de faire en sorte que le produit de convolution linéaire (produit de covolution “classique”) et le produit de convolution circulaire soient identiques en prolongeant les signaux de longueur \(N\) par au moins \(N\) zéros.
Property 3.2 (TF discrète en fréquences)
Tout comme le signal numérique ne peut pas être à temps continu, il ne sera possible de calculer qu’un nombre fini d’échantillons de la TFD. Cela a deux conséquences : une mauvaise résolution de la TFD observée, qui pourra être améliorée en utilisant une méthode d’interpolation comme le zero padding, et un signal qui devra être considéré comme périodique en temporel par transformée de Fourier inverse, ce qui aura pour effet de transformer un produit en produit de convolution circulaire (entre signaux périodisés).
3.1.5. Expressions de la TFD et de la TFD inverse#
Les trois approximations précédemment étudiées (échantillonnage temporel, limitation de la durée du signal et échantillonnage fréquentiel) conduisent finalement à l’outil suivant pour calculer la transformée de Fourier en numérique :
Definition 3.2 (TFD)
Le même cheminement conduirait à obtenir l’expression de la TFD inverse :
Definition 3.3 (TFD inverse)
Notons que, dans ces expressions, \(x(k)\) est une notation simplifiée pour \(x(kT_e)\), de même que \(X(n)\) est une notation simplifiée pour \(X\left(n\frac{F_e}{N}\right)\). Ils représentent respectivement le \(k^{ieme}\) élement du tableau de points de signal et le \(n^{ieme}\) élement du tableau de points de la TFD du signal. On utilisera ces notations par la suite.
