3.2. Propriétés de la TFD

\label{sec_proprietes}

3.2.1. Linéarité

Property 3.3 (Linearité)

La transformée de Fourier est linéaire :

\[ TFD\left[x_1(k)+\lambda x_2(k)\right] = TFD\left[x_1(k)\right]+\lambda TFD\left[x_2(k)\right], \; \lambda \; scalaire. \]

3.2.2. Translation

Property 3.4 (Translation \(\Rightarrow\) rotation de phase)

Une translation dans le domaine temporel entraine un déphasage dans le domaine fréquentiel :

\[TFD\left[x(k-k_0)\right] = TFD\left[x(k)\right] e^{-j 2 \pi \frac{k_0n}{N}} = X(n) e^{-j 2 \pi \frac{k_0n}{N}}\]

Proof.

\[\begin{align*} TFD[x(k-k_0)] & = \sum_{k=k_0}^{N-1+k_0} x(k-k_0)e^{-j 2 \pi \frac{kn}{N}} \\ &= \sum_{m=0}^{N-1} x(m)e^{-j 2 \pi \frac{(m+k_0)n}{N}} \\ &=e^{-j 2 \pi \frac{k_0n}{N}}X(n) \end{align*}\]

3.2.3. Symétrie Hermitienne

Property 3.5 (Symétrie Hermitienne)

Soit \(X(n)\) la transformée de Fourier discrète d’un signal réel \(x(k)\), on a :

\[ X\left(N-n\right) = X(-n) = X^*(n) \]

Proof. Si \(x(k)\) réel alors \(x^*(k)=x(k)\) et \(X(-n) = \sum_{k=0}^{N-1} x(k)e^{j 2 \pi \frac{kn}{N}}=\left[\sum_{k=0}^{N-1} x(k)e^{-j 2 \pi \frac{kn}{N}}\right]^*=X^*(n)\).

D’autre part \(X\left(N-n\right)=\sum_{k=0}^{N-1} x(k)e^{-j 2 \pi \frac{k(N-n)}{N}}=\sum_{k=0}^{N-1} x(k)e^{j 2 \pi \frac{kn}{N}}=X(-n)\).

3.2.4. Convolution circulaire

Le produit de convolution linéaire (“classique”) est donné en numérique par :

\[ \left(x_1 \ast x_2\right) (k)=\sum_{p=0}^{N-1}x_1(p)x_2\left(k-p\right) \]

Property 3.6 (Convolution circulaire)

la transformée de Fourier discrète ne transforme pas un produit en produit de convolution linéaire mais en produit de convolution circulaire (entre signaux périodisés) :

\[ X_1(n) X_2(n) \; \underrightarrow{TFD^{-1}} \; \left(x_1 \otimes x_2\right)(k)=\sum_{p=0}^{N-1}x_1(p)x_2\left([k-p]_{modulo \; N}\right) \]

si \(X_1(n)\) est la transformée de Fourier discrète de \(x_1(k)\) et \(X_2(n)\) la transformée de Fourier discrète \(x_2(k)\).

Proof.

\[\begin{align*} TFD^{-1}\left[X_1(n) X_2(n)\right]&=\frac{1}{N} \sum_{n=0}^{N-1} X_1(n)X_2(n) e^{j 2 \pi \frac{kn}{N}}\\ &= \frac{1}{N} \sum_{n=0}^{N-1} \left(\sum_{p=0}^{N-1} x_1(p)e^{-j 2 \pi \frac{pn}{N}}\right) \left(\sum_{q=0}^{N-1} x_2(q)e^{-j 2 \pi \frac{qn}{N}}\right) e^{j 2 \pi \frac{kn}{N}}\\ &=\frac{1}{N} \sum_{p=0}^{N-1} \sum_{q=0}^{N-1} x_1(p) x_2(q) \sum_{n=0}^{N-1} e^{-j 2 \pi \frac{ln}{N}}, \; \text{avec} \; l=p+q-k. \end{align*}\]

Or nous avons :

\[\begin{split}\sum_{n=0}^{N-1} e^{-j 2 \pi \frac{ln}{N}}=\left\{\begin{array}{ll} 0 & \hbox{$l\neq iN$} \\ N & \hbox{$l=iN \Leftrightarrow q=k-p+iN$}. \end{array} \right.\end{split}\]

Ce qui donne bien :

\[TFD^{-1}\left[X_1(n) X_2(n)\right]=\sum_{p=0}^{N-1} x_1(p)x_2\left(\left[k-p\right]_{\text{modulo N}}\right)=\left(x_1 \otimes x_2\right)(k)\]

Les figures Fig. 3.7 et Fig. 3.8 illustrent la différence entre un produit de convolution linéaire et un produit de convolution circulaire sur un exemple considérant deux signaux de \(N=3\) points : \(x_1=\left[1 \; 2 \;3\right]\) et \(x_2=\left[1 \;1 \;1\right]\). Le produit de convolution linéaire considère que les signaux sont nuls en dehors de leurs \(N\) points (Fig. 3.7), tandis que le produit de convolution circulaire considère des signaux périodisés ( Fig. 3.8). On constate que les résultats des ces deux produits de convolution sont différents : \(\left[0 \;1 \;3 \;6 \;5 \;3 \; 0\right]\) pour le produit de convolution linéaire et \(\left[6 \; 6 \; 6 \; 6 \; 6 \; 6\; 6\right]\) pour le produit de convolution circulaire.

Fig. 3.7 Produit de convolution linéaire entre les signaux \(x_1=\left[1 \; 2 \;3\right]\) et \(x_2=\left[1 \;1 \;1\right]\).

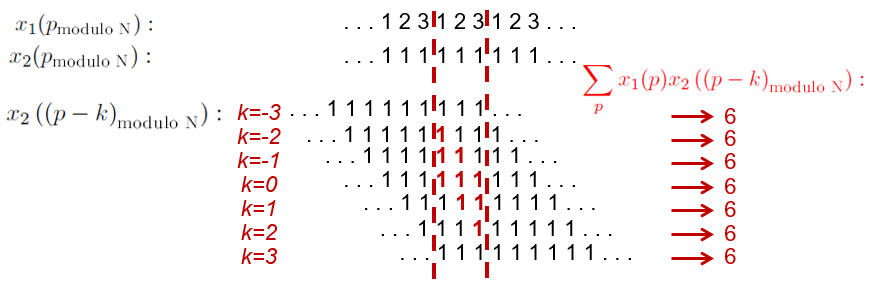
Fig. 3.8 Produit de convolution circulaire entre les signaux \(x_1=\left[1 \;2 \;3\right]\) et \(x_2=\left[1 \;1 \;1\right]\).

Néanmoins, il est possible de rendre le résultat du produit de convolution circulaire égal à celui du produit de convolution linéaire en prolongeant les signaux par un nombre de zéros au moins égal au nombre de point de signal (Fig. 3.9).

Fig. 3.9 Produit de convolution circulaire = Produit de convolution linéaire entre les signaux \(x_1=\left[1 \;2 \;3\right]\) et \(x_2=\left[1 \;1 \;1\right]\).

3.2.5. Egalité de Parseval

Property 3.7 (Egalité de Parseval)

\[ \sum_{k=0}^{N-1}|x(k)|^2=\frac{1}{N}\sum_{n=0}^{N-1}|X(n)|^2 \]

Proof.

\[\begin{align*} \sum_{k=0}^{N-1}|x(k)|^2&=\sum_{k=0}^{N-1}x(k)x^*(k)=\sum_{k=0}^{N-1}x(k) \frac{1}{N}\sum_{n=0}^{N-1}X^*(n)e^{-j 2 \pi \frac{kn}{N}}\\ &=\frac{1}{N}\sum_{n=0}^{N-1}X^*(n) \sum_{k=0}^{N-1}x(k)e^{-j 2 \pi \frac{kn}{N}}=\frac{1}{N}\sum_{n=0}^{N-1}X^*(n)X(n)\\ &=\frac{1}{N}\sum_{n=0}^{N-1}\left|X(n)\right|^2 \end{align*}\]

3.2.6. Algorithme de calcul rapide

La transformée de Fourier discrète se prête à un algorithme de calcul rapide que l’on nomme FFT pour “Fast Fourier Transform”. Son principea , détaillé au paragraphe suivant, consiste à décomposer le signal de départ (sur \(N\) points) en une succession de sous suites entrelacées en effectuant à chaque étape de l’algorithme des transformées de Fourier disjointes sur les points d’indices pairs et les points d’indices impairs du tableau représentant le signal numérique. La condition de départ est que le nombre de points \(N\) soit une puissance de \(2\).