1.2. Numérisation du signal : Quantification

Definition 1.4

Un signal quantifié est un signal dont les amplitudes ne peuvent prendre qu’un nombre fini de valeurs.

1.2.1. Quantification uniforme : principe, impact

Chaque valeur du signal sera approchée par un multiple entier d’une quantité élémentaire appelée pas de quantification. Le nombre de valeurs possibles, pour l’amplitude du signal après quantification, va être donné par le nombre de bits de quantification, utilisés : avec \(\mathrm{nb}\) bits on pourra coder \(2^{nb}\) niveaux sur la dynamique \(D\) du signal. Dans le cas d’une quantification uniforme (pas de quantification \(q\) constant sur toute la dynamique du signal), le pas de quantification est donné par : \(q=\frac{D}{2^{nb}}\). La Fig. 1.2 présente un exemple de quantification uniforme d’une fonction sinusoïdale.

Fig. 1.2 Exemple de sinusoïde quantifiée.

Plusieurs types de quantification existent. On peut, par exemple, affecter tous les échantillons de signal appartenant à un niveau donné à la valeur min de ce niveau (quantification par troncature : on approche par \(nq\) toutes les valeurs de signal comprises entre \(nq\) et \((n+1)q\)) ou bien affecter à la valeur \(nq\) toutes les valeurs de signal comprises entre \(\left(n-\frac{1}{2}\right)q\) et \(\left(n+\frac{1}{2}\right)q\) (quantification par arrondi). Dans tous les cas, l’opération de quantification est une opération non linéaire irréversible. Cependant, si elle est effectuée dans de bonnes conditions (pas d’écrétage du signal, pas de quantification suffisamment fin) elle est équivalente à l’ajout d’un bruit, \(n_Q(t)\), sur le signal non quantifié de départ \(x(t)\) pour donner le signal quantifié \(x_Q(t)\) (voir Fig. 1.3 pour un exemple):

\[x_Q(t)=x(t)+n_Q(t),\]

Fig. 1.3 Erreur, ou bruit, de quantification.

Ce bruit peut être modélisé comme un signal aléatoire de moyenne nulle, suivant une loi uniforme sur \(\left[-\frac{q}{2}, \; \frac{q}{2}\right]\) et le rapport signal à bruit de quantification s’écrit :

\[SNR_Q(dB)=10 \log_{10}\left(\frac{P_x}{P_{n_Q}}\right)\]

où

\[P_{n_Q}=E\left[n_Q^2\right]=\int_{\mathbb{R}} n_Q^2 p_{n_Q} dn_Q=\int_{-\frac{q}{2}}^{\frac{q}{2}} n_Q^2 \times \frac{1}{q} dn_Q=\frac{q^2}{12}\]

ce qui conduit à

\[SNR_Q(dB)=6 \; nb+ constante,\]

où la constante dépend du signal considéré (voir Exercise 1.6).

A l’heure actuelle, du fait du nombre de bits de quantification disponibles sur les processeurs, cette opération s’avère alors quasi transparente.

Definition 1.5 (Bruit de quantification)

L’opération de quantification est donc une opération irréversible mais si elle est effectuée dans de bonnes conditions (pas d’écrétage du signal, pas de quantification suffisamment fin) elle est équivalente à l’ajout d’un bruit sur le signal non quantifié de départ, avec un rapport signal à bruit de quantification qui s’écrit \(SNR_Q(dB)=6 \; nb+ constante\), où \(nb\) est le nombre de bit de quantification utilisé et la constante dépend du signal considéré.

1.2.2. Quantification non uniforme

Afin de diminuer le nombre de bits nécessaires pour quantifier un signal, il faudrait pouvoir adapter le pas de quantification à l’amplitude du signal d’entrée. On a alors une quantification non uniforme. En pratique cette opération est réalisée en utilisant une compression avant quantification uniforme, de manière à amplifier les faibles amplitudes et à minimiser l’effet des fortes amplitudes. Deux lois de compression sont normalisées et utilisées : la loi \(A\) et la loi \(\mu\). Ce sont deux approximations de la loi logarithmique utilisée pour les signaux audio dans les applications traitant la voix humaine. L’échantillon de signal, \(y\), en sortie de la compression est donné, en fonction de l’échantillon du signal en entrée \(x\), par :

• Loi \(A\):

  \[\begin{align*} y &=sgn(x) \frac{A \left|x\right|}{1+\ln\left(A \right)} \quad 0\leq \left|x\right| \leq \frac{1}{A}\\ &=sgn(x) \frac{1+\ln\left(A \left|x\right|\right)}{1+\ln\left(A \right)} \quad \frac{1}{A}\leq \left|x\right| \leq 1 \end{align*}\]

  La loi \(A\) est utilisée principalement en Europe avec un paramètre de compression de \(87,6\). Elle permet, en téléphonie par exemple, d’utiliser \(8\) bits de quantification au lieu des \(12\) qui seraient nécessaires avec un quantifieur uniforme étant donnée la dynamique du signal à quantifier (Fig. 1.4).

  

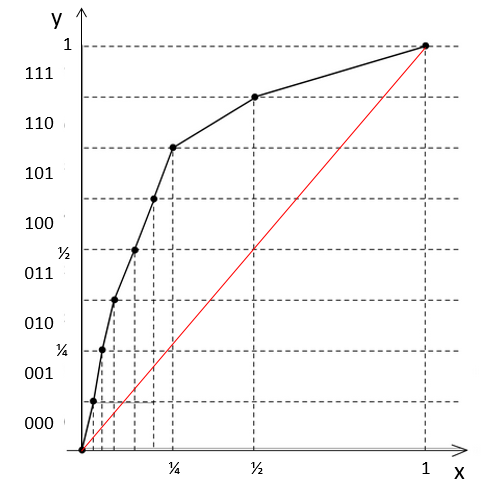
  Fig. 1.4 Caractéristique de compression à 13 segments (loi \(A\))

• Loi \(\mu\) :

  \[y = sgn(x) \frac{\ln \left(1+ \mu \left|x\right|\right)}{\ln\left(1+ \mu\right)}, \; -1\leq x \leq 1,\]

  utilisée principalement aux États-Unis et au Japon avec \(\mu=255\).