4.1. Calcul dans le domaine temporel

4.1.1. Signaux déterministes

Definition 4.1 (Intercorrélation, cas déterministe )

Le \(k^{\text{ième}}\) échantillon de la fonction d’intercorrélation numérique entre les signaux \(x\) et \(y\) s’écrit :

• Pour un signal déterministe à énergie finie :

\[R_{xy}(k)=\sum_{n=-\infty}^{+\infty}x(n)y^{*}(n-k)\]

• pour un signal déterministe à puissance moyenne finie périodique de période \(N_0\) :

\[R_{xy}(k)=\frac{1}{N_0}\sum_{n=0}^{N_0-1}x(n)y^{*}(n-k)\]

• pour un signal déterministe à puissance moyenne finie non périodique :

\[R_{xy}(k)=\underset{N \rightarrow + \infty}{\lim}\frac{1}{2N+1} \sum_{n=-N}^{N}x(n)y^{*}(n-k)\]

4.1.2. Signaux aléatoires

Definition 4.2 (Intercorrélation, cas aléatoire)

Le \(k^{\text{ième}}\) échantillon de la fonction d’intercorrélation numérique entre les signaux aléatoires \(x\) et \(y\) s’écrit :

\[ R_{xy}(k)=\mathbb{E}\left[x(n)y^{*}(n-k)\right] \]

4.1.2.1. Estimateur biaisé

En supposant le signal ergodique et en utilisant un estimateur de la moyenne, le \(k^{\text{ième}}\) élément de la fonction d’intercorrélation numérique entre les signaux aléatoires \(x\) et \(y\) pourra être estimé de la manière suivante :

\[ \widehat{R}_{xy}(k)=\frac{1}{N}\sum_{n=0}^{N-1}x(n)y^{*}(n-k) \]

si \(N\) représente le nombre de points des signaux considérés.

En réalité, si on considère les signaux numériques comme des tableaux de \(N\) points (\(\left[x(0) \; ... \; x(N-1)\right]\) et \(\left[y(0) \; ... \; y(N-1)\right]\)), la somme précédente porte sur \(N-k\) échantillons du produit \(x(n)y^{*}(n-k)\) (signaux décalés, produit non nul uniquement entre \(k\) et \(N-1\)). L’estimateur précédent est donc, en réalité, donné par :

Definition 4.3 (Estimateur biaisé)

\[ \widehat{R}_{xy}(k)=\frac{1}{N}\sum_{n=k}^{N-1}x(n)y^{*}(n-k) \]

et il est biaisé :

\[ \mathbb{E}\left[\widehat{R}_{xy}(k)\right]=\frac{N-|k|}{N}R_{xy}(k). \]

Le biais est ici multiplicatif et triangulaire (voir figure Fig. 4.1 dans les exemples).

4.1.2.2. Estimateur non biaisé

Afin de supprimer le biais, on peut définir un deuxième estimateur temporel de la manière suivante :

Definition 4.4 (Estimateur non biaisé)

\[ \widehat{R}_{xy}(k)=\frac{1}{N-k}\sum_{n=0}^{N-1}x(n)y^{*}(n-k)\quad 0\leq k\leq N-1 \]

On a bien alors

\[\mathbb{E}\left[\widehat{R}_{xy}(k)\right]=R_{xy}(k)\]

Cependant cet estimateur possède une grande variance sur les bords. En effet, lorsque \(k \rightarrow N\) peu de points vont être utilisés pour réaliser l’estimation. Celle-ci variera donc beaucoup entre différentes réalisations de signal (voir Fig. 4.2 dans les exemples). Ceci reste vrai avec l’estimateur biaisé mais le phénomène est masqué par le fait que le biais soit triangulaire.

4.1.2.3. Exemples : cosinus, ligne d’image SAR (Synthese Aperture Radar)

La Fig. 4.1 trace une estimation biaisée de la fonction d’autocorrélation (\(x=y\)) d’un cosinus, obtenue grâce à la fonction xcorr.m de matlab. On voit apparaitre le biais multiplicatif triangulaire.

La Fig. 4.2 trace une estimation non biaisée de la fonction d’autocorrélation d’un cosinus, obtenue grâce à la fonction xcorr.m de matlab, avec le paramètre ‘unbiased’. On voit apparaitre la variance de l’estimation sur les bords de la fenêtre d’analyse.

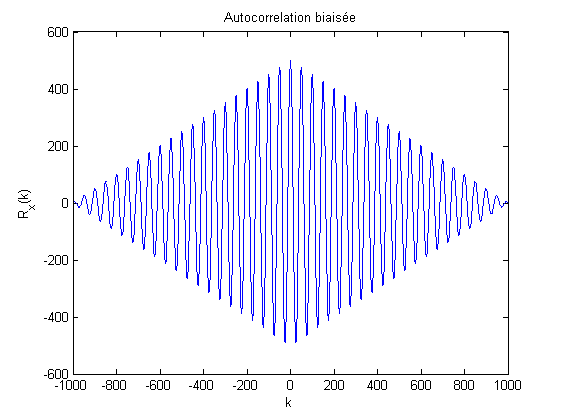
Fig. 4.1 Estimation biaisée de la fonction d’autocorrélation du cosinus.

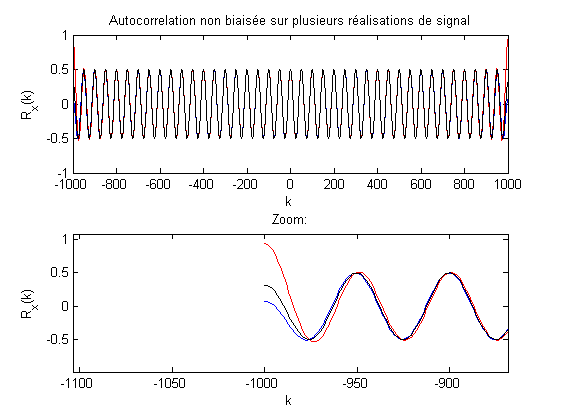
Fig. 4.2 Estimations non biaisées de la fonction d’autocorrelation du cosinus.

La Fig. 4.3 compare les estimations biaisée et non biaisée de la fonction de covariance (\(autocorrelation-moyenne^2\)) d’un signal réel (ligne d’image SAR (Synthese Aperture Radar)) à la covariance théorique. On constate que la covariance estimée avec un estimateur biaisé semble donner un résultat plus proche de la covariance théorique que la covariance estimée avec un estimateur non biaisé. Cette constatation reste généralement vraie pour les signaux réels. Notons que pour une comparaison valable des estimateurs biaisés et non biaisés, il faudrait comparer leur erreur quadratique moyenne. Il a été montré que, dans de nombreux cas en effet, l’erreur quadratique moyenne de l’estimateur biaisé est nettement inférieure à celle de l’estimateur non biaisé. Dans les deux cas cependant, on peut améliorer les estimations en augmentant la durée d’observation. L’estimateur biaisé est, en effet, asymptotiquement non biaisé, tandis que la variance de l’estimateur non biaisé apparait sur les bords.

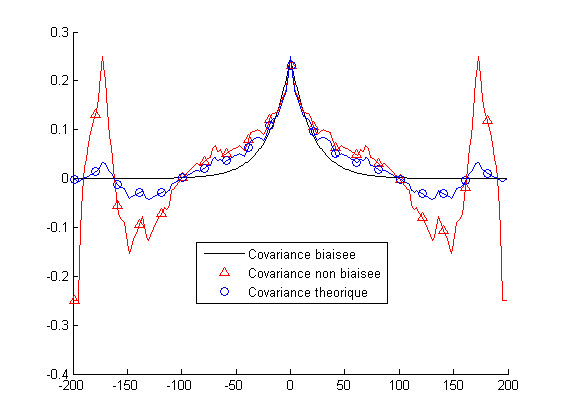
Fig. 4.3 Estimations de la covariance sur une ligne d’image SAR.