Synthèse des filtres numériques rationnels
Contents
7.7. Synthèse des filtres numériques rationnels#
Definition 7.10
La synthèse d’un filtre numérique correspond au passage entre les spécifications à respecter et l’ensemble des coefficients définissant le filtre numérique.
Les spécifications à respecter correspondent à un gabarit que l’on se donne sur la réponse en fréquence du filtre et qui fixe des marges dans lesquelles elle doit se trouver.
Les synthèses des filtres RIF et RII se font de manière très différente (cf plus loin).}
7.7.1. Introduction#
Notion de gabarit
Le gabarit à respecter pour le filtre à synthétiser correspond à la définition des marges dans lesquelles la réponse en fréquence du filtre synthétisé doit se trouver.
Les figures Fig. 7.2 et Fig. 7.3 montrent un exemple de gabarit donné sur le module de la réponse en fréquence pour un filtrage de type passe-bas.
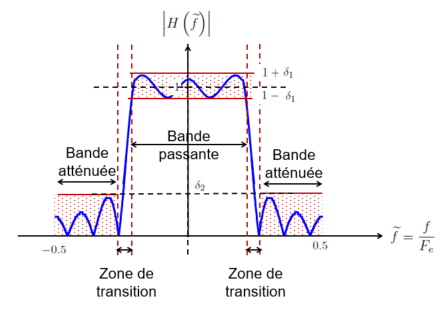
Fig. 7.2 Exemple de gabarit à respecter (en rouge) pour un filtre passe-bas.#
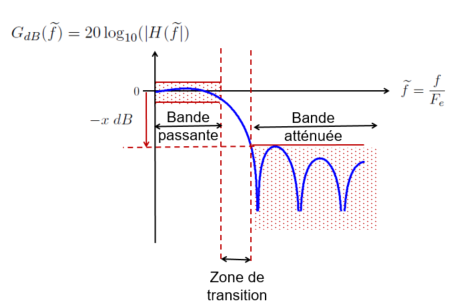
Fig. 7.3 Exemple de gabarit (en dB) à respecter (en rouge) pour un filtre passe-bas.#
Réponses en fréquences idéales cibles pour la synthèse
La figure Fig. 7.4 présentent les \(4\) réponses en fréquence idéales classiques : pour un filtre passe-bas qui laisse passer les fréquences autour de \(0\) (“basses fréquences”) jusqu’à la fréquence \(\widetilde{f}_c\) (fréquence de coupure normalisée), pour un filtre passe-haut qui coupe les fréquences autour de \(0\) (“basses fréquences”) jusqu’à la fréquence \(\widetilde{f}_c\) et laisse passer les fréquences au-delà de \(\widetilde{f}_c\) (“hautes fréquences”), pour un filtre passe-bande qui ne laisse passer que les fréquences se trouvant sur une certaine bande (entre \(\widetilde{f}_{c_1}\) et \(\widetilde{f}_{c_2}\)) et coupe toutes les autres, pour un filtre coupe-bande (ou réjecteur) qui laisse passer toutes les fréquences sauf celles se trouvant entre \(\widetilde{f}_{c_1}\) et \(\widetilde{f}_{c_2}\).
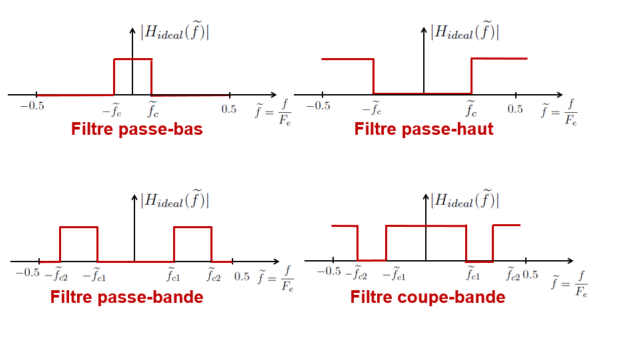
Fig. 7.4 Réponse en fréquences idéales (cibles pour la synthèse).#
Remark 7.2 (Filtre idéal et filtrage en temsp réel)
Nous pouvons envisager en numérique de réaliser un filtrage idéal : on calcule le spectre de notre signal (TFD), on met à \(0\) dans le tableau correspondant toutes les fréquences que l’on souhaite éliminer puis on revient au signal filtré par TFD inverse. Cependant, ce filtrage ne se fait pas en temps réel car ils sous entend que l’on dispose de tout les échantillons de signal pour en calculer le spectre. Or, dans le cadre d’une transmission, les échantillons de signal sont envoyés et arrivent les uns après les autres (toutes les \(T_e\) secondes si \(T_e\) représente la période d’échantillonnage). Un filtrage ne pourra être réalisé en temps réel que s’il est réalisé dans le domaine temporel, en implantant l’expression \( y(n) =-\sum_{k=1}^{M-1} a_k y(n-k) + \sum_{k=0}^{N-1} b_k x(n-k)\) ou l’expression \( y(n) =\sum_{k=0}^{N-1} b_k x(n-k)\), selon que l’on souhaite réaliser un filtre de type RII ou bien de type RIF et en s’assurant que le calcul de la/des somme(s) puisse se faire en \(T_e\) secondes. C’est cette implantation dans le domaine temporel qui va conduire, comme nous allons le voir par la suite, à un filtrage qui sera non idéal et donc à la nécessité de définir un gabarit à respecter. Notons également qu’il n’y aura pas un filtre unique respectant le gabarit. On pourra choisir celui qui satisfait le mieux aux critères que l’on se donne (le plus simple d’implantation, celui qui présente la charge de calcul la plus faible, le plus stable numériquement …)
7.7.2. Synthèse des filtres à réponse impulsionnelle finie#
7.7.2.1. Synthèse par développement en série de Fourier#
La synthèse de filtres RIF est assez intuitive et facile à mettre en oeuvre. On se donne une réponse en fréquences idéale, \(H_I(\widetilde{f})\), du filtre à réaliser et un gabarit à respecter. On travaille en numérique, on doit donc considérer que la réponse en fréquence est périodique de période \(1\) en fréquences normalisées (TF d’une réponse impulsionnelle échantillonnée). Un filtre RIF peut donc être synthétisé directement par un développement en série de Fourier de la réponse en fréquence idéale :
où les coefficients de la série de Fourier \(h_I(k)\) représentent les échantillons de la réponse impulsionnelle, ou “coefficients” \(b_k\), définissant le filtre :
\(h_I\left( k\right) \) représente ici le k\(^{\text{ième}}\) point de la reponse impulsionnelle \(h_I(t)\) du filtre qui est échantillonnée avec une période d’échantillonnage \(T_e=\frac{1}{F_e}\) (il s’agit en réalité de \(h_I(kT_e)\)).
En pratique le nombre de coefficients de la réponse impulsionnelle devra être limité. En effet celle-ci sera représentée par un tableau contenant un nombre fini de valeurs. On modélise cette limitation par l’application d’une fenêtre de troncature, \(w(n)\), sur la réponse impusionnelle idéale. Cela conduit à la réponse impulsionnelle réelle suivante :
et donc à une réponse en fréquence qui n’est plus idéale :
En effet, cette convolution de la réponse en fréquence idéale par la transformée de Fourier de la fenêtre de troncature va générer des transitions adoucies et des oscillations autour des transitions (voir tracé en bleu dans la figure Fig. 7.2. Nous retouvons les mêmes phénomènes que ceux déjà évoqués dans le chapitre sur la transformée de Fourier d’un signal de durée limitée.
Lorsque l’on conserve tout simplement un certain nombre de points de la réponse impulsionnelle idéale pour former la réponse impulionnelle réelle : \(\left[h_I(-N) ... h_I(N)\right]\), c’est comme si on utilisait une fenêtre de troncature rectangulaire. Dans les autres cas nous avons une pondération de la réponse impulsionnelle idéale, en plus de la troncature : \(\left[h_I(-N)w(-N) ... h_I(N)w(N)\right]\), en supposant que l’on conserve \(2N+1\) éléments de \(h_I(k)\) et que l’on utilise une fenêtre de troncature, \(w\), de \(2N+1\) échantillons : \(\left[w(-N) ... w(N)\right]\).
Definition 7.11 (Synthèse d’un filtre RIF)
**Le nombre de points conservé sur la réponse impulsionnelle idéale pour former le tableau représentant la réponse impulsionnelle réelle est appelé ORDRE du filtre. Les éléments du tableau représentant la réponse impulsionnelle réelle sont appelés COEFFICIENTS du filtre.
La synthèse d’un filtre RIF va alors consister à déterminer l’ordre du filtre, ainsi que la fenêtre de troncature à utiliser, afin que celui-ci satisfasse au gabarit souhaité.**
Les figures Fig. 7.5 et Fig. 7.6 présentent des exemples d’influence de l’ordre et de la fenêtre de troncature utilisée dans la cas d’un filtrage passe-bas.
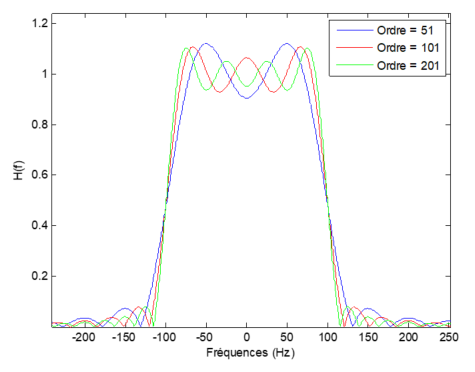
Fig. 7.5 Exemple d’influence de l’ordre dans la synthèse d’un filtre RIF de type passe-bas - Fenêtre rectangulaire.#
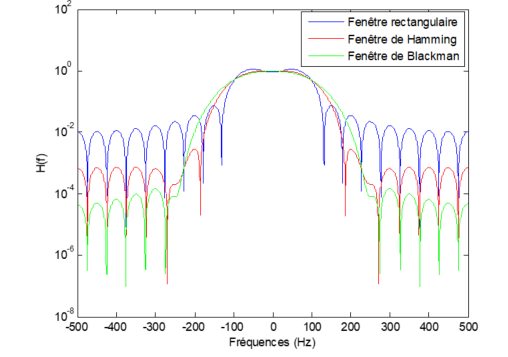
Fig. 7.6 Exemple d’influence de la fenêtre de troncature dans la synthèse d’un filtre RIF de type passe-bas - Ordre = \(21\).#
Attention
la réponse impulsionnelle obtenue doit être causale pour que le filtre soit réalisable. Si elle ne l’est pas en sortie de la synthèse on doit la décaler afin qu’elle le devienne et, ce faisant, on introduit un retard
Ce décalage ne modifie pas le module de la réponse en fréquence mais ajoute une phase linéaire en fréquence, qui ne fera qu’ajouter un facteur constant au temps de propagation de groupe (pas de dégroupage).
En supposant \(N\) pair et en notant \(H_{causal}(\widetilde{f})=TFD\left[h_{causal}(n)\right]\), on a :
et donc :
Remark 7.3
Il existe un calcul (très approximatif) permettant de se donner un ordre de départ pour la synthèse : \(\text{Ordre} = \frac{2}{3} log_{10}\left(\frac{1}{\delta_1 \delta_2}\right)\frac{F_e}{\Delta f}\), où \(2 \delta_1\) représente la largeur admise autour de \(1\) en bande passante (en linéaire pas en dB), \(\delta_2\) représente l’atténuation minimum en bande coupée (en linéaire pas en dB) et \(\Delta f\) représente la largeur de la zone de transition.
En général le choix de la fenêtre fixe l’amplitude des oscillations et, pour une fenêtre donnée, l’ordre (\(2N+1\)) va fixer la largeur de la zone de transition. Comme cela a été vu dans le chapitre sur la transformée de Fourier, on retrouve ici le compromis à réaliser entre la largeur de la transition et l’amplitude des oscillations : une fenêtre qui permet d’avoir des oscillations de plus faible amplitude, comparée à une autre, fournit une zone de transition plus large pour un même ordre. Les caractéristiques des principales fenêtres sont résumées dans le tableau suivant :
Caractéristiques des fenêtres de troncature
\[\begin{split} \begin{array}{ |c || c | c |} \hline \text{Type} & \text{Largeur} & \text{Attenuation min} \\ \text{fenêtre} & \text{zone de transition } (\Delta \omega) & \text{en bande coupée (en dB)} \\ \hline \hline \mathrm{Rectangulaire} & \frac{1.8 \pi}{Ordre} & 21 \\ \hline \mathrm{Barlett} & \frac{5.6 \pi}{Ordre} & 25 \\ \hline \mathrm{Hanning} & \frac{6.2 \pi}{Ordre} & 44 \\ \hline \mathrm{Hamming} & \frac{6.6 \pi}{Ordre} & 53 \\ \hline \mathrm{Blackman} & \frac{11 \pi}{Ordre} & 74 \\ \hline \mathrm{Kaiser } (\beta=4.54) & \frac{5.8 \pi}{Ordre} & 50 \\ \hline \mathrm{Kaiser } (\beta=5.67) & \frac{7.8 \pi}{Ordre} & 60 \\ \hline \end{array} \end{split}\]Les résultats obtenus par synthèse directe peuvent être ensuite optimisés grâce, par exemple, à la méthode des moindres carrés (minimisation au sens des moindres carrés de la distance entre le gabarit désiré et le gabarit du filtre obtenu par la synthèse en série de Fourier, fonction firls.m sous Malab) ou à l’algorithme de Remez (pour obtenir la meilleure approximation du gabarit présentant des ondulations d’amplitude constante, fonction firgr.m sous Malab).
Il existe des fonctions matlab fournissant les coefficients du filtre souhaité sans avoir à réaliser le calcul de la impulsionnelle (voir, par exemple, fir1.m pour les filtres “classiques” ou rcosdesign.m pour réaliser un filtre en cosinus surélevé très utilisé en transmission). Il est également possibe de rentrer la réponse en fréquence souhaitée comme un tableau de point et d’obtenir la réponse impulsionnelle correspodante en utilisant la TFD inverse (ifft.m sous Matlab).
7.7.2.2. Avantages/Inconvénients des filtres RIF#
Les filtres RIF sont fréquemment désignés par le terme de filtres non-récursifs, car ils ne présentent pas de boucle de réaction de la sortie vers l’entrée, ce qui assure leur stabilité de manière inconditionnelle (pour peu que les coefficients du filtre soient bornés).
Les filtres RIF peuvent avoir très simplement un temps de propagation de groupe constant. En effet :
Si
\[Arg \left[H(\widetilde{f})\right]=\text{constante}\]alors
\[Arg\left[H_{causal}(\widetilde{f})\right]=\text{constante}-\pi \widetilde{f} N\]Et donc :
\[TPG(\widetilde{f})=-\frac{1}{2 \pi}\frac{dArg\left[H_{causal}(\widetilde{f})\right]}{d\widetilde{f}}=\frac{N}{2}\]Or \(Arg \left[H(\widetilde{f})\right]\) est constant si la réponse impulsionnelle \(h(n)\) est paire ou impaire :
\[\begin{align*} Arg \left[H(\widetilde{f})\right] &= Arg \left[\sum_{-\infty}^{+\infty} h(n) \left(\cos\left(2 \pi \widetilde{f} n \right)+j \sin\left(2 \pi \widetilde{f}n\right)\right)\right]\\ &= atan\left(\frac{\sum_{-\infty}^{+\infty} h(n) \sin\left(2 \pi \widetilde{f} n \right)}{\sum_{-\infty}^{+\infty} h(n) \cos\left(2 \pi \widetilde{f} n \right)}\right)\\ &= \left\{ \begin{array}{rl} 0 & \mbox{si } h(n) pair\\ \frac{\pi}{2} & \mbox{si } h(n) impair. \\ \end{array} \right. \; \end{align*}\]La synthèse des filtres RIF est très simple.
Certains gabarits très contraints peuvent nécessiter l’utilisation de beaucoup trop de coefficients et donc un temps de calcul beaucoup trop élevé. Dans ce cas on utilisera plutôt un filtre de type RII.
7.7.3. Synthèse des filtres à réponse impulsionnelle infinie#
7.7.3.1. Principe de la méthode#
Les filtres RII sont des filtres qui présentent une boucle de réaction de la sortie vers l’entrée (filtres récursifs). L’idée de leur synthèse est de s’appuyer sur les bibliothèques très fournies de modèles pour le filtrage analogique.
La synthèse de filtre analogique consiste, à partir d’un gabarit défini sur la réponse en fréquence souhaitée \(H(f)\), à choisir un modèle dans la bibliothèque de modèles et à adapter ses paramètres de façon à obtenir un filtre satisfaisant au gabarit. Elle fournit une fonction de transfert en \(p\) : \(H(p)\).
En numérique le gabarit est donné sur \(H(\tilde{f})\) et nous souhaitons obtenir une fonction de transfert en \(z\) : \(H(z)\).
Il “suffirait” donc de trouver un “passage” entre \(H(\tilde{f})\) et \(H(f)\), puis entre \(H(p)\) et \(H(z)\) pour utiliser ce qui existe en synthèse analogique à des fins numériques.
7.7.3.2. Mise en pratique#
La figure Fig. 7.7 résume la manière de réaliser une synthèse de filtre RII. Les explications sont données dans la suite.
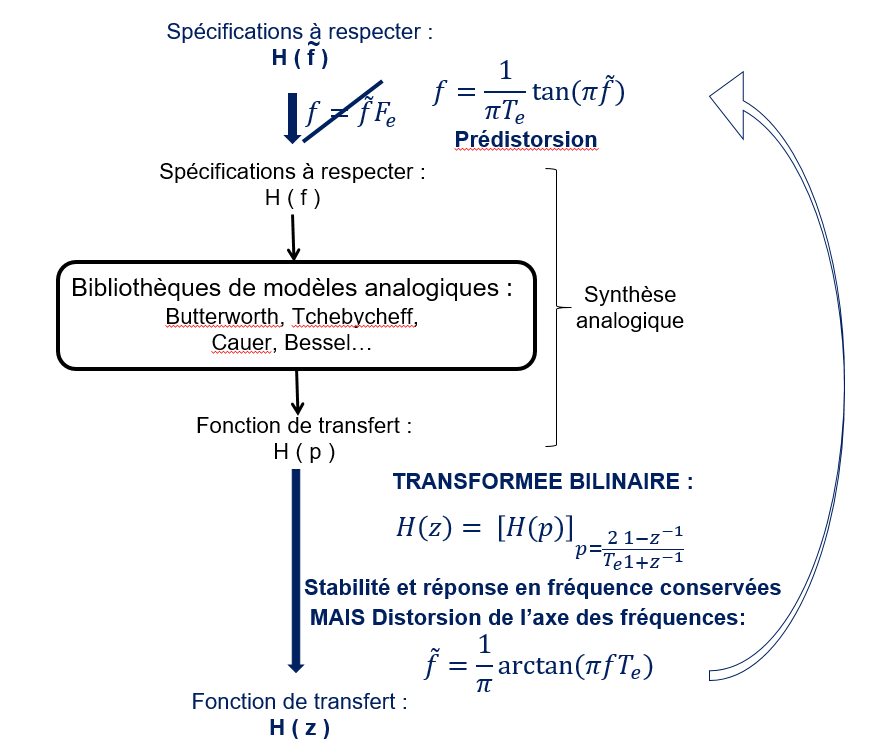
Fig. 7.7 Méthode de synthèse d’un filtre numérique rationnel de type RII (filtre récursif).#
Le passage entre \(H(\tilde{f})\) et \(H(f)\) qui semble naturel est de prendre : \(f=\tilde{f} F_e\). Nous allons cependant voir par la suite qu’il va falloir le modifier.
Le passage entre \(H(p)\) et \(H(z)\) doit permettre de conserver au filtre numérique la stabilité et la conformité au gabarit fixé obtenue à l’issue de la synthèse analogique. Pour cela on doit trouver une transformée du plan des \(p\) vers le plan des \(z\) qui transforme :
o le demi plan gauche (lieu de stabilité en analogique : pôles de \(H(p)\) à parties réelles négatives) en l’intérieur du cercle unité (lieu de stabilité en numérique : pôles de \(H(z)\) de modules inférieurs à \(1\))
o l’axe imaginaire (lieu de parcours de la réponse en fréquence en analogique : \(H(f)=\left[H(p)\right]_{p=j \omega = j 2 \pi f}\)) en le cercle unité (lieu de parcours de la réponse en fréquence en numérique : \(H(\widetilde{f})=\left[H(z)\right]_{z=e^{j 2 \pi \widetilde{f}}}\)).
Cette transformée est la transformée bilinéaire. Elle est obtenue par approximation numérique de l’opérateur intégrale définissant le passage dans le filtre analogique (voir figure \ref{TBilin}) et donne \(H(z)\), à partir de \(H(p)\) de la manière suivante :
\[ H\left( z\right)=\left[H(p)\right]_{p=\frac{2}{T_e}\frac{1-z^{-1}}{1+z^{-1}}} \]
Fig. 7.8 Obtention de la transformée bilinéaire.#
Attention cependant car, même si la transformée bilinéaire permet de passer de \(H(p)\) à \(H(z)\) en conservant la stabilité et la réponse en fréquence du filtre, elle ne transforme pas les fréquences \(f\) en \(\widetilde{f}=\frac{f}{F_e}\).
En effet, quand \(p=j 2 \pi f\) alors
On a bien transformé l’axe imaginaire en le cercle unité mais pas \(f\) en \(\widetilde{f}=\frac{f}{F_e}\).
En écrivant
on obtient
Ceci n’est néanmoins pas génant car il suffit de passer du gabarit sur \(H(\tilde{f})\) au gabarit sur \(H(f)\), non pas en faisant \(f=\tilde{f} F_e\) mais en faisant
La distorsion de l’axe des fréquences introduite par la transformée bilinéaire est ainsi compensée par une prédistorsion lors du passage de \(H(\tilde{f}) \) vers \(H(f)\).
Une fois établis les passages de \(H(\tilde{f}) \) vers \(H(f)\) et de \(H(p)\) vers \(H(z)\), on constate donc que la synthèse analogique revient à faire une synthèse analogique : choix du modèle et adaptation des paramètres pour satisfaire au gabarit.
Definition 7.12 (Synthèse des filtres RII)
A partir du gabarit numérique souhaité (sur \(H(\widetilde{f})\)), on détermine un gabarit analogique (sur \(H(f)\)) en conservant les amplitudes mais en prédistordant les fréquences de la manière suivante :
Le gabarit obtenu permet de réaliser une synthèse analogique, en utilisant les bibliothèques très fournies de modèles disponibles.
Une fois la fonction de transfert analogique, \(H(p)\), satisfaisant au gabarit obtenue, on déduit la fonction de transfert numérique \(H(z)\) en appliquant la transformée bilinéaire :
Cette transformée conserve la stabilité et la réponse en fréquence du filtre mais provoque une distorsion de l’axe des fréquence qui a été pré-compensée au départ.
Parmi les modèles analogiques les plus courants on trouve :
Le modèle de Butterworth, qui est le plus simple :
\[\left|H(f)\right|^2=\frac{1}{1+\left(\frac{f}{f_c}\right)^{2n}}, \text{ où } f_c \text{ représente la fréquence de coupure}\]Ce modèle ne présente pas d’ondulations, ni en bande passante, ni en bande atténuée.
L’ordre du filtre \(n\) permet de régler la raideur de la transition entre la bande passante et la bande atténuée.
La zone de transition est plus large qu’avec les autres modèles pour un même ordre mais la phase de la réponse en fréquence est modéremment non linéaire (TPG à peu près constant sur la bande passante).
Le modèle de Tchebychef (ou Chebyshev) présente des ondulations en bande passante ou en bande atténuée (type I ou type II), ce qui permet une zone de transition plus étroite qu’un modèle de Butterworth pour un même ordre. La phase de la réponse en fréquence est, par contre, non linéaire (TPG non constant).
Le modèle de Cauer (ou Elliptique) présente des ondulations en bande passante et en bande atténuée, ce qui permet une zone de transition encore plus étroite que les modèles précédents pour un même ordre. La phase de la réponse en fréquence est, pour ce modèle aussie, non linéaire (TPG non constant).
Le modèle de Bessel présente une phase à peu près linéaire pour la réponse en fréquence, ne présente pas d’ondulations ni en bande passante ni en bande atténuée mais sa zone de transition va être beaucoup plus large que les autres filtres pour un même ordre. C’est un filtre de phase.
Des exemples de synthèse de filtres RII se trouvent dans la section exercices (corrections dans le poly exercices et problèmes résolus). Notons que de nombreuses fonctions sont proposées par Matlab pour réaliser une synthèse de RII en utilisant les différents modèles issus des bibliothèques analogiques.
7.7.3.3. Avantages/Inconvénients des filtres RII#
Du fait de la présence de pôles dans leur fonction de transfert (boucle de réaction), les filtres RII présentent des risques d’instabilité.
Le temps de propagation de groupe des filtres RII n’est pas constant. Néanmoins , selon le modèle analogique utilisé, le TPG sera plus ou moins perturbé en bande passante.
La synthèse des filtres RII est plus complexe que celle des filtres RIF.
Le principal avantage des filtres RII va être de satisfaire certains gabarits avec un côut calculatoire plus faible que les filtres RIF (ordre, ou nombre de coefficients nécessaires, moins élevé).
