Exercices
7.9. Exercices#
Exercise 7.1
On considère un filtre de fonction de transfert :
où \(a\) et \(b\) sont deux réels \(\in ]0,1[\) avec \(b>a\).
Quel est l’ordre du filtre défini par la fonction de transfert \(H(z)\) ?
Déterminer l’équation récurrente définissant le filtre dans le domaine temporel.
Quel type de filtre rationnel (RIF, RII) est défini par \(H(z)\)? Justifiez votre réponse.
Le filtre défini par \(H(z)\) est il stable ? Justifiez votre réponse.
Déterminer la réponse impulsionnelle \(h(n)\) permettant de pouvoir réaliser le filtre.
Exercise 7.2
Soit le filtre d’entrée \(x(n)\) et de sortie \(y(n)\) défini par l’équation récurrente suivante :
Déterminer sa fonction de transfert \(H(z)\).
Déterminer la transformée en z de \(\delta(n)\) et de \(\delta(n-1)\), où \(\delta(n)\) represente le Dirac numérique :
\[\begin{split} \delta(n) = \left\{ \begin{array}{rl} 1 & \mbox{for } n=0\\ 0 & \mbox{for } n\neq 0. \\ \end{array} \right. \; \end{split}\]En déduire la réponse impulsionnelle du filtre.
Déterminer la transformée en z de la fonction échelon unité \(u(n)\), ainsi que son domaine d’existence. En déduire la réponse indicielle du filtre (réponse à un échelon).
Le filtre défini par l’équation (7.1) est il un filtre RIF ou un filtre RII ? Justifiez votre réponse.
Le filtre défini par l’équation (7.1) est il stable ? Justifiez votre réponse.
Le filtre défini par l’équation (7.1) est il causal ? Justifiez votre réponse.
Exercise 7.3 (synthèse d’un filtre passe-bas de type RIF)
On veut synthétiser un filtre passe-bas en essayant d’approcher par un filtre RIF la fonction de tranfert idéale de la figure Fig. 7.14. Donner l’expression de la réponse impulsionnelle d’un filtre à \(2N+1\) coefficients utilisant une fenêtre rectangulaire de troncature et d’un filtre à \(2N+1\) coefficients utilisant une fenêtre de troncature de Hamming donnée par \(w(n)=0.54+0.46 \cos(\frac{2 \pi n}{2N+1})\).
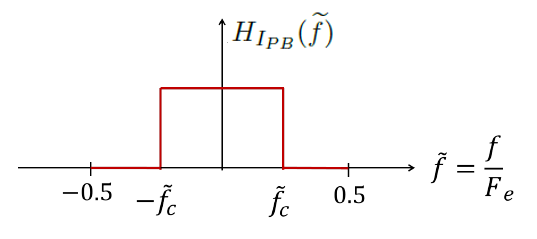
Fig. 7.14 Filtre passe-bas - Fonction de transfert idéale#
Exercise 7.4 (Etude de la cellule du second ordre )
Cellule du second ordre purement récursive
On la définit par l’équation aux différences suivantes :
\[y(n)=x(n)-a_1y(n-1)-a_2y(n-2)\]Exprimez sa fonction de transfert en z.
Dans le plan des coefficients (\(a_1\) en abscisse, \(a_2\) en ordonnées), tracez le domaine de stabilité du filtre.
Donnez l’expression de la réponse en fréquence en fonction de \(a_1\) et \(a_2\).
A quelle condition existe-t-il une pulsation de résonance \(\widetilde{\omega}_0\) (\(\widetilde{\omega}=2 \pi \widetilde{f}\)) ?
Montrez que la valeur du module de la réponse harmonique à la résonance est inversement proportionnelle à la distance des pôles au cercle de rayon \(1\). On se placera dans le cas où \(a_1^2 <4 a_2\) (vraie cellule du second ordre) et on écrira la réponse en fréquence en \(\widetilde{\omega}_0\) sous forme polaire. On donne :
\[\left|H(\widetilde{\omega}_0)\right|=\frac{2 \sqrt{a_2}}{(1-a_2)\sqrt{4a_2-a_1^2}}\]Donnez l’expression de la réponse impulsionnelle en fonction des coordonnées polaires \(r\) et \(\theta\) des pôles dans le cas où \(a_1^2 <4 a_2\).
Proposez une structure de réalisation de ce filtre.
Cellule du second ordre générale
On considère une équation générale de la cellule du second ordre :
\[y(n)=x(n)+b_1x(n-1)+b_2x(n-2)-a_1y(n-1)-a_2y(n-2)\]Exprimez sa fonction de transfert en z.
Montrez que cette cellule du second ordre peut être considérée comme la mise en cascade de la cellule purement récursive précédente et d’un filtre RIF.
En déduire une structure de réalisation.
Pour \(b_2=1\) montrez que la phase du RIF est linéaire.
Exercise 7.5 (Synthèse RII guidée)
On se propose de synthétiser un filtre passe-bas numérique de type RII. Le gabarit à respecter est donné par la figure Fig. 7.15. Afin de simplifier les calculs la fréquence d’échantillonnage sera considérée égale à \(1\)Hz.
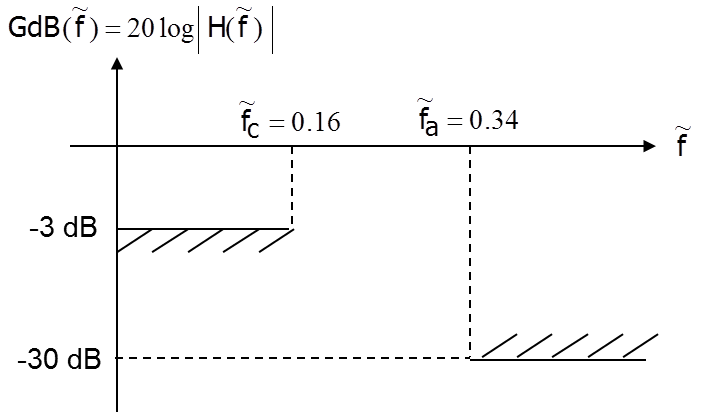
Fig. 7.15 Gabarit numérique à respecter#
La synthèse de filtre RII est une méthode de synthèse numérique qui utilise la synthèse analogique. Cette synthèse analogique a besoin en entrée d’un gabarit analogique à respecter. On passera donc dans un premier temps du gabarit numérique sur \(H(\widetilde{f})\) au gabarit d’entrée de la synthèse analogique portant sur \(H(f)\). Tracez le gabarit à respecter par \(H(f)\).
Réalisation de la synthèse analogique :
a. Première étape : on doit choisir une fonction modèle analogique et régler ses paramètres afin de satisfaire le gabarit souhaité. On impose dans cet exercice d’utiliser le modèle passe-bas de Butterworth, dont la fonction de transfert est donnée par :
\[\left|H(\omega)\right|^2=\frac{1}{1+\left(\frac{\omega}{\omega_c}\right)^{2N}},\]où \(\omega_c\) représente la pulsation de coupure. Montrez que le paramètre \(N\) permettant au modèle de Butterworth de satisfaire le gabarit à moindre coût est égal à \(3\).
b. Deuxième étape : passer de \(\left|H(\omega)\right|^2\) à \(H(p)\).
\[\left|H(\omega)\right|^2=\left[\left|H(p)\right|^2\right]_{p=j\omega}\]d’où pour \(N=3\) :
\[\left|H(p)\right|^2=\frac{1}{1-p^6}=H(p)H(-p)\](on oublie pour l’instant le \(\frac{1}{\omega_c}\), sachant qu’on remplacera \(p\) par \(\frac{p}{\omega_c}\) à la fin).
Parmi les \(6\) pôles de \(\left|H(p)\right|^2\) (qui sont les racines sixièmes de l’unité), \(3\) appartiennent à \(H(p)\), \(3\) appartiennent à \(H(-p)\). On choisira comme pôles pour \(H(p)\) : \(p_0=-1\), \(p_1=-\frac{1}{2}-j\frac{\sqrt{3}}{2}\), \(p_2=-\frac{1}{2}+j\frac{\sqrt{3}}{2}\). Expliquez ce qui conduit à ce choix. On en déduit donc la fonction de transfert suivante :
\[H(p)=\frac{1}{(p+1)(p^2+p+1)}\]soit en remplaçant \(p\) par \(\frac{p}{\omega_c}\) :
\[H(p)=\frac{\omega_c^3}{(p+\omega_c)(p^2+p\omega_c+\omega_c^2)}\]c. Troisième étape : Application de la transformée bilinéaire. Après application de la transformée bilinéaire sur \(H(p)\) on obtient la fonction de transfert suivante :
\[H(z)=H_1(z)H_2(z)\]avec
\[H_1(z)=\frac{0.43(1+z^{-1}}{1-0.29z^{-1}}, \quad H_2(z)=\frac{0.135+0.27z^{-1}+0.135z^{-2}}{1-0.753z^{-1}+0.4z^{-2}}\]Le filtre obtenu est il stable ? Justifiez votre réponse.
Le filtre obtenu est il résonnant ? Justifiez votre réponse.
On souhaite filtrer un signal \(x\) en utilisant le filtre RII synthétisé. En appelant \(y\) le signal de sortie, proposer un programme matlab permettant de passer de \(x\) à \(y\). Ce programme pourra être testé pour filtrer des sinusoïdes lors des séances de TP.
