7.2. Définitions#

7.2.1. Linéarité#

Definition 7.1 (Linéarité)

Si \(y_1(n)\) et \(y_2(n)\) sont les sorties du filtre qui correspondent respectivement aux entrées \(x_1(n)\) et \(x_2(n)\), le filtre est linéaire s’il fait correspondre \(y_1(n)+y_2(n)\) à une entrée \(x_1(n)+x_2(n)\).

7.2.2. Invariance temporelle#

Definition 7.2 (Invariance temporelle)

Si \(y(n)\) est la sortie du filtre qui correspond à l’entrée \(x(n)\), le filtre est dit invariant dans le temps s’il fait correspondre \(y(n-n_0)\) à l’entrée \(x(n-n_0)\), \(n_0\) représentant un retard de \(n_0\) échantillons.

7.2.3. Réponse impulsionnelle et fonction de transfert#

On peut écrire tout signal numérique de la manière suivante :

\[x(n)=\sum_{k=-\infty}^{+\infty}x(k) \delta(n-k)\]

où \(\delta(n)\) représente le Dirac numérique qui vaut \(1\) pour \(n=0\) et \(0\) ailleurs.

Si on note \(h(n)\) la sortie du filtre correspondant à l’entrée \(\delta(n)\) et \(y(n)\) la sortie du filtre correspondant à \(x(n)\), alors du fait de la linéarité et de l’invariance temporelle nous obtenons pour tout signal numérique \(x(n)\), placé à l’entrée d’un filtre numérique linéaire invariant dans le temps, une réponse \(y(n)\) donnée par :

\[ y(n)=\sum_{k=-\infty}^{+\infty} h(n-k)x(k)=\sum_{k=-\infty}^{+\infty}h(k) x(n-k)=x(n) \ast h(n)\]

On peut donc écrire toute sortie \(y(n)\) d’un filtre numérique linéaire invariant dans le temps en fonction de l’entrée appliquée \(x(n)\) et de \(h(n)\) qui est appelée réponse impulsionnelle du filtre (réponse à une impulsion représenté par \(\delta(n)\)). Cette réponse impulsionnelle \(h(n)\) définit donc le filtre. Sa transformée en z, \(H(z)\), est appelée fonction de transfert du filtre. Si \(Y(z)\) et \(X(z)\) sont respectivement les transformées en z de \(y(n)\) et \(x(n)\), on a alors :

\[H(z)=\frac{Y(z)}{X(z)}=TZ\left[h(n)\right]\]

D’où la représentation d’un filtre numérique linéaire invariant dans le temps :

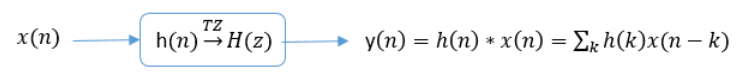
_images/FLIT.png

Fig. 7.1 Filtre numérique linéaire invariant dans le temps#

7.2.4. Filtres numériques rationnels#

Les filtres numériques rationnels sont définis par une fonction de transfert rationnelle en z (par analogie avec les filtres analogiques qui, eux, sont définis par une fonction de transfert rationnelle en p) :

\[ H(z) =\frac{\sum_{k=0}^{N-1} b_k z^{-k}}{\sum_{k=0}^{M-1} a_k z^{-k}} \]

Un filtre numérique rationnel est ainsi défini par deux vecteurs de coefficients : \(A=\left[a_0 \; a_1 ... \; a_{M-1}\right]\) et \(B=\left[b_0 \; b_1 ... \; b_{N-1}\right]\) stockés en mémoire. On pourra, par exemple, réaliser le filtrage sous Matlab en utilisant la fonction filter.m de la manière suivante : y=filter(B,A,x), si x représente le signal à filtrer, y le signal filtré et B et A les tableaux de coefficients définissant le filtre à utiliser. Nous reviendrons par la suite plus en détail sur cette catégorie de filtres.

7.2.5. Réponse en fréquence et temps de propagation de groupe (TPG)#

La réponse en fréquence, ou réponse harmonique, du filtre est donnée par :

Definition 7.3 (Réponse en fréquence ou réponse harmonique)

\[ H(\widetilde{f})=\left[H(z)\right]_{z=e^{j 2 \pi \widetilde{f}}} \]

où \(\widetilde{f}=\frac{f}{F_e}\) (fréquence normalisée), avec \(F_e\) qui représente la fréquence d’échantillonnage.

On peut également écrire :

\[\left|H(\widetilde{f})\right|^2=\left[H(z)H\left(\frac{1}{z}\right)\right]_{z=e^{j 2 \pi \widetilde{f}}}\]

ce qui peut faciliter certains calculs (voir exercices).

Le temps de propagation de groupe (TPG) est donné en fréquences normalisées par :

Definition 7.4 (Temps de propagation de groupe (TPG))

\[TPG(\widetilde{f})=-\frac{1}{2 \pi}\frac{d\varphi_H(\widetilde{f})}{d\widetilde{f}}, \; \text{avec} \; \varphi_H(\widetilde{f})=Arg\left[H(\widetilde{f})\right]\]

\(TPG(\widetilde{f})\) représente le temps que met un paquet d’onde à la fréquence \(\widetilde{f}\) pour traverser le filtre. Lorsque l’on souhaite réaliser un filtre numérique les spécifications portent généralement sur le module de sa réponse en fréquence et on souhaite un TPG le plus constant possible, au moins sur la/les bande(s) passante(s). Notons cependant qu’il existe des filtres de phase, pour lesquels les spécifications portent sur la phase de la réponse en fréquence (afin de corriger, par exemple, un TPG non constant).