7.8. Implantation des filtres numériques rationnels

Comme nous l’avons évoqué précédemment, un filtrage numérique ne pourra être réalisé en temps réel que s’il est réalisé dans le domaine temporel, en implantant les expressions :

\[ y(n) =-\sum_{k=1}^{M-1} a_k y(n-k) + \sum_{k=0}^{N-1} b_k x(n-k) \; \text{ pour un filtre RII} \]

\[ y(n) =\sum_{k=0}^{N-1} b_k x(n-k) \; \text{ pour un filtre RIF} \]

Ces expressions, définissant un filtre numérique dans le domaine temporel, s’appuient sur \(3\) opérations élémentaires : le retard, la multiplication et l’addition. La fonction de transfert d’un système numérique effectuant un retard de \(T_e\) (un coup d’échantillonnage) étant \(z^{-1}\), il est d’usage de représenter les retards unités dans les schémas bloc d’implantation des filtres par la notation \(z^{-1}\).

7.8.1. Structure directe

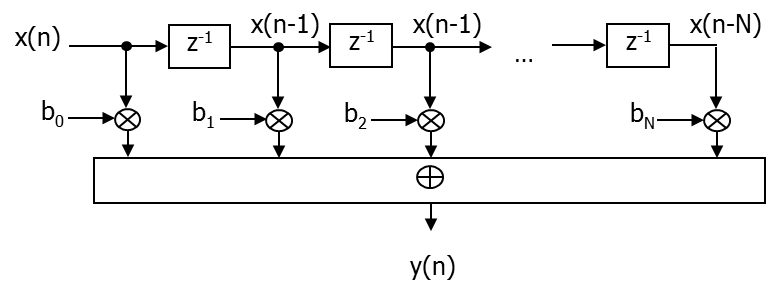
La structure la plus directe pour implanter un filtre numérique rationnel est donné par le schéma de la figure Fig. 7.9. Cette implantation nécessite deux files d’attente et \(\sim M+N+1\) opérations d’additions/multiplications. Il est cependant possible de n’utiliser qu’une seule file d’attente : c’est la structure canonique présentée dans le paragraphe suivant.

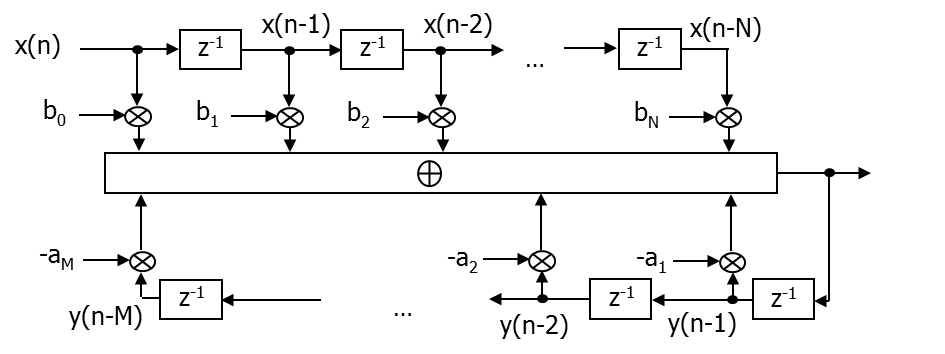
Fig. 7.9 Structure directe.

7.8.2. Structure canonique

En utilisant une variable intermédiaire :

\[W(z)=\frac{X(z)}{\sum_{k=0}^{M-1} a_k z^{-k}}\]

on obtient \(y(n)=\sum_{k=0}^{N-1} b_k w(n-k)\) avec \(w(n)=-\sum_{k=1}^{M-1} a_k w(n-k)+x(n)\), et donc une structure d’implantation simplifiée, dite canonique et présentée dans la figure Fig. 7.10. Cette implantation ne nécessite qu’une seule file d’attente et \(\sim M+N+1\) opérations d’additions/multiplications.

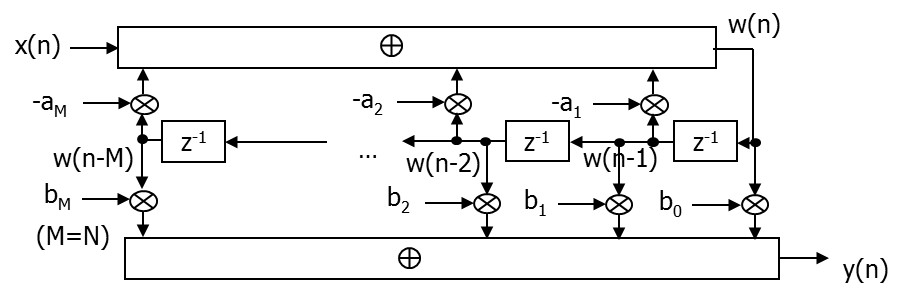
Fig. 7.10 Structure canonique.

7.8.3. Structures décomposées

La plupart du temps on implante un filtre numérique en le décomposant en cellules du premier et du deuxième ordre. L’implantation peut se faire de deux manières : en série ou en parallèle.

7.8.3.1. Structure décomposée en série (ou cascade)

La figure Fig. 7.11 illustre la structure d’implantation par décomposition série. Elle est obtenue en exprimant la fonction de transfert globale du filtre comme un produit de fonctions de transfert plus simples :

\[H(z)=G\prod_{i=0}^{M-1}H_i(z)\]

où \(G\) est une constante et les \(H_i(z)\) sont des cellules du premier et du deuxième ordre de la forme :

\[H_i(z)=\frac{b_0+b_1z^{-1}}{1+a_1z^{-1}}\]

ou

\[H_i(z)=\frac{b_0+b_1z^{-1}+b_2z^{-2}}{1+a_1z^{-1}+a_2z^{-2}}\]

obtenues en factorisant le numérateur et le dénominateur de \(H(z)\). Les cellules du premier ordre ont des pôles et des zéros réels, tandis que les cellules du second ordre ont des zéros et des pôles qui sont complexes conjugués, les coefficients \(a_k\) et \(b_k\) eux sont toujours réels.

Fig. 7.11 Structure série.

7.8.3.2. Structure décomposée en parallèle

La figure Fig. 7.12 représente une décomposition parallèle. Elle est obtenue en exprimant la fonction de transfert globale du filtre comme une somme de fonctions de transfert plus simples :

\[H(z)=G+\sum_{i=0}^{M-1}H_i(z)\]

où \(G\) est une constante et les \(H_i(z)\) sont des cellules du premier et du deuxième ordre de la forme :

\[H_i(z)=\frac{b_0}{1+a_1z^{-1}}\]

ou

\[H_i(z)=\frac{b_0+b_1z^{-1}}{1+a_1z^{-1}+a_2z^{-2}}\]

obtenues en décomposant \(H(z)\) en éléments simples.

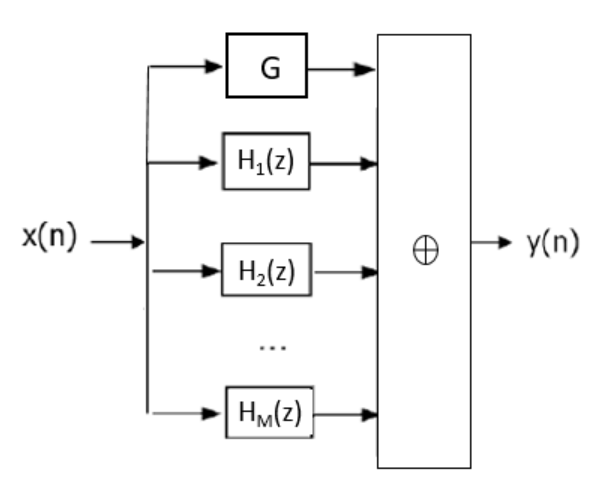
Fig. 7.12 Structure parallèle.

7.8.4. Structure non récursive

Il s’agit de la structure des filtres à réponses impulsionnelles finies, ou filtres RIF. Elle est représentée dans la figure Fig. 7.13.

Fig. 7.13 Structure non récursive.