3.3. Algorithme de calcul rapide (FFT) de Cooley Tuckey

3.3.1. Principe

La transformée de Fourier de départ \(X(n)\) porte sur les \(N\) points d’un signal numérique \(x(k)\) :

\[ X(n)=\sum_{k=0}^{N-1}x(k)e^{-j 2 \pi \frac{kn}{N}}=\sum_{k=0}^{N-1}x(k)W_N^{-kn}, \; n=0,...,N-1 \]

en notant \(W_N=e^{j \frac{2 \pi }{N}}\). On parle de TFD d’ordre \(N\). Son temps de calcul est évalué à \(N^2\) operations d’additions/multiplications.

On suppose que \(N\) est une puissance de \(2\) : \(N=2^p\) et on va commencer à décomposer le signal en sous suites entrelacées.

3.3.1.1. Première décomposition

\[ X(n)=X_1(n) + W_N^{-n} X_2(n), \; n=0,...,N-1, \]

où

\[ X_1(n)=\sum_{i=0}^{N/2-1}x(2i)W_{N/2}^{-in}, \quad X_2(n)=\sum_{i=0}^{N/2-1}x(2i+1)W_{N/2}^{-in}, \quad i=0,...,N/2-1 \]

On peut évaluer le temps de calcul suite à cette première décomposition à \(2 \left(\frac{N}{2}\right)^2 + N\) operations d’additions/multiplications, ce qui est déjà \(\ll N^2\), surtout si \(N\) est grand.

3.3.1.2. Deuxième décomposition

\[ X_1(n)=X_{11}(n) + W_{N/2}^{-n} X_{12}(n), \; \quad X_2(n)=X_{21}(n) + W_{N/2}^{-n} X_{22}(n), \quad n=0,...,N/2-1, \]

où :

\[ X_{11}(n)=\sum_{i=0}^{N/4-1}x_1(2i)W_{N/4}^{-in}, \quad X_{12}(n)=\sum_{i=0}^{N/4-1}x_1(2i+1)W_{N/4}^{-in}, \quad i=0,...,N/4-1 \]

\[ X_{12}(n)=\sum_{i=0}^{N/4-1}x_2(2i)W_{N/4}^{-in}, \quad X_{22}(n)=\sum_{i=0}^{N/4-1}x_2(2i+1)W_{N/4}^{-in}, \quad i=0,...,N/4-1 \]

avec \(x_1(p)=x(2i)\) et \(x_2(p)=x(2i+1), \; i,p=0,...,N/2-1\).

…

3.3.1.3. Dernière décomposition

On continue jusqu’à arriver à la plus petite transformée de Fourier possible qui porte sur deux points et que l’on appelle le “papillon” de la transformée de Fourier numérique (Fig. 3.10).

On aura alors réalisé \(Np\) transformées de Fourier d’ordre \(2\) ou “papillons”, soit un temps de calcul de \(\mathbf{N log_2(N)\ll N^2}\) opérations d’additions/multiplications.

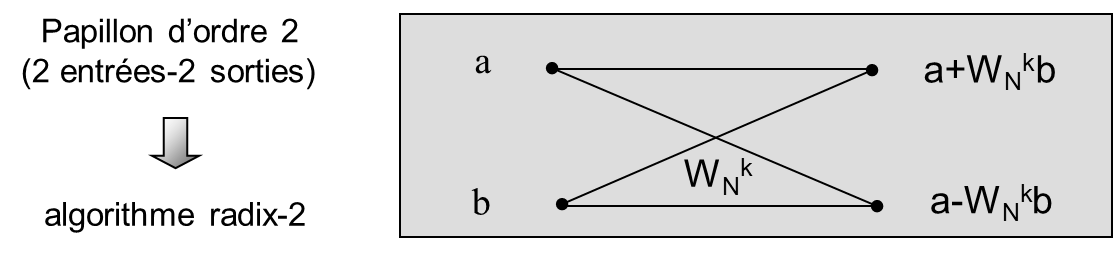
Fig. 3.10 Papillon de la FFT : transformée de Fourier d’ordre \(2\) = \(2\) opérations d’addition/multiplication.

3.3.2. Exemple pour \(N=2^3=8\)

3.3.2.1. Première décomposition

\[ X(n)=X_1(n) + W_8^{-n} X_2(n), \; n=0,\cdots,7, \]

où \(X_1(n)\) porte sur \(x(0),x(2),x(4),x(6)\) et \(X_2(n)\) porte sur \(x(1),x(3),x(5),x(7)\).

3.3.2.2. Deuxième et dernière décomposition

\[ X_1(n)=X_{11}(n) + W_{4}^{-n} X_{12}(n), \; n=0,\cdots,3, \]

où \(X_{11}(n)\) porte sur \(x(0),x(4)\) et \(X_{12}(n)\) porte sur \(x(2),x(6)\).

\[ X_2(n)=X_{21}(n) + W_{4}^{-n} X_{22}(n), \; n=0,\cdots,3, \]

où \(X_{21}(n)\) porte sur \(x(1),x(5)\) et \(X_{22}(n)\) porte sur \(x(3),x(7)\).\

3.3.2.3. Graphe correspondant

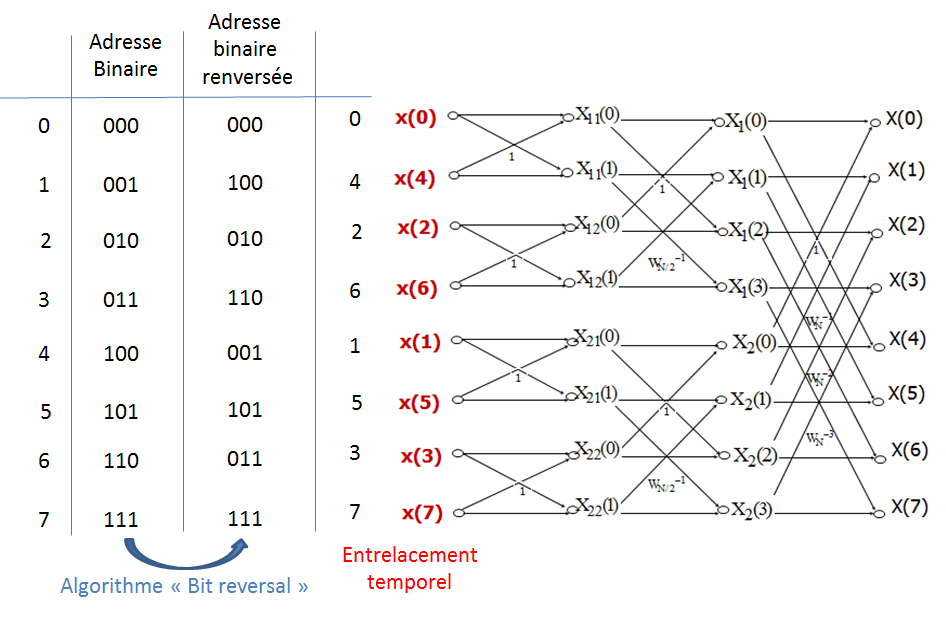
Fig. 3.11 Graphe de la FFT pour \(N=2^3\).

On a \(p=3\) colonnes de \(\frac{N}{2}=4\) papillons, soit \(p\times\left(\frac{N}{2}\right)\times 2 = pN = log_2(N)N = 3 \times 8 =24\) opérations d’additions multiplications, au lieu de \(N^2=64\) si nous n’avions pas utilisé l’algorithme de FFT. On remarque que les échantillons de signal ne se présentent pas dans leur ordre naturel à l’entrée de l’algorithme. On peut utiliser un algorithme de renversement de l’adresse binaire (“bit reversal”) afin de les présenter dans l’ordre voulu.